Quantum States
Pentagons and triangles give a way to get past these
esoteric philosophical arguments to more practical
considerations. Specifically, to model these
superposition states from a computational viewpoint,
think of a quantum bit $\psi$ that is both
$\ket{0}$ and $\ket{1}$ at the same time as shown
below:
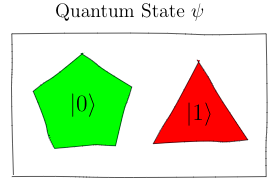
The pentagons and triangles indicate that the quantum bit $\psi$
is in two states at the same time. But, as with the cat in the
box, the moment you try to ascertain its state, it randomly
collapses to either the classical $\ket{0}$ bit or a
the $\ket{1}$ state.
The quantum state $\psi$ above has a single pentagon and a single
triangle. In general, however, a quantum state can have several
pentagons and triangles, and some may even be rotated.
For example, the quantum state below has seven $\ket{0}$ pentagons
and three inverted $\ket{1}$ triangles:

The only restriction is that quantum states are made up of only
pentagons and triangles. No other shapes are allowed.
There is one important point I'd like to make here. You
never actually see a quantum bit in two states.
Whenever you try to examine its state, it
collapses to one of the two states: $\ket{0}$ or $\ket{1}$.
The exact state it collapses to depends on the ratio of
pentagon $\ket{0}$ vs. triangle $\ket{1}$ shapes. The
more of one than the other increases the odds of qubit
collapsing to one state over the other.
A quantum state always collapses
to a classical state, 0 or 1. Thus, whatever rotation
a pentagon $\ket{0}$ or a triangle $\ket{1}$ qubelet may
have had in the quantum state, that information is
lost when the qubit collapses to a classical bit.
The fact that quantum states collapse to classical
states seems like a letdown especially if you were
hoping to see some sort of array which holds
all possible solutions to your problem, like the
sensational press may have you believe. But, it's
actually a good thing that quantum states are
totally invisible to us and the only concrete we
deal with are classical bits. This means that
the results of a quantum computation match reality.
The major mental shift when writing quantum
algorithms is learning to manipulate quantum
states so that they collapse to the solution
you want.
With these two concepts, in the next section, you'll
write computer instructions that manipulate the quantum
states to do calculations like those of classical computers
but with one difference — these computations are
blindingly fast.
NOTE
The shape of the qubelet, pentagon or triangle, has no mathematical or physical significance. That the pentagon has a symmetry of 5 versus a 3 for the triangle has no bearing on physical reality. I've simply used these shapes to vividly illustrate a $\ket{0}$ quantum state from that of a $\ket{1}$ state to help fix ideas in the text.
Where to learn more
The material in this section has been adapted from Chapter 4 of my book. In this chapter, you'll also learn how to write a quantum program for the concepts you've learned about here. In chapter 6, you'll see the connection between the pictures you see here and the formal way way quantum states are represented mathematically.