From Bits to Qubits
Qubits, or quantum bits, are the equivalent of
classical bits that drives quantum computing.
But, unlike their classical counterparts,
quantum bits are tricky to describe.
Almost all textbooks, articles or explainer
videos immediately jump to math to define qubits
as if the key to understanding them lies in
unraveling abstruse equations. The usual
approach makes quantum computing feel as an
alien landscape for most computer programmers
even though it’s applied to traditional
computational tasks. Without properly motivating
the intuition quantum mechanics brings to bear,
designing algorithms that capitalize on them to
solve hard problems that are out of reach of
today’s computers, is frustrating.
Although the behavior of quantum bits are governed by quantum mechanics,
from a quantum computing standpoint, their actions can be
boiled down to commonplace operations.
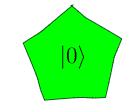
To fix ideas, I use a pentagon for a $\ket{0}$ qubit:
And, a triangle for a $\ket{1}$ qubit:
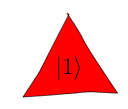
We'll call these shapes qubelets. So we'll call the
pentagon shape represeting a $\ket{0}$ qubit a
$\ket{0}$ qubelet. Likewise a triangle $\ket{1}$ is
called a $\ket{1}$ qubelet.
When these shapes represent classical bits, their
orientations are always fixed.
With quantum bits, these shapes
rotate. For example, a triangle $\ket{1}$ qubelet that's
rotated, say, $45^{\circ}$ anti-clockwise is shown below:

A triangle $\ket{1}$ qubelet rotated $180^{\circ}$
so that it's upside down is:
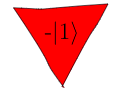
This qubit is mathematically written with a negative
sign $-\ket{1}$.
This ability of a quantum bit to rotate is the
first difference from a classical bit. Pairs of
qubelets, in which one is rotated $180^{\circ}$
from the other, cancel out and are removed
from the quantum state. This behavior has no
classical equivalent.
This seemingly minute difference plays a pivotal role in
making quantum computers so much more powerful than classical
computers.
Another difference between a qubit and a classical
bit that leads to hyper-fast computations is the
ability of qubits to be in
two states at the same time. That is, their ability
to be suspended in a superposition of both
$\ket{0}$ and $\ket{1}$ states.
What does this really mean? How can something be two things
at the same time?
You may have heard of Schrödinger's
cat in a closed box. Someone outside the box
wouldn't have a clue whether the cat is dead or alive.
So, for this person, their lack of knowledge allows
them to think of the cat as being in two
states — dead or alive. It's only when the
box is opened would they know if the cat is breathing.
This concept of superposition sounds thrilling but it's
not apparent how it could solve problems.
So how exactly does one go about making any sense of
superposition when designing a computer algorithm to
solve a real world application?
Where to learn more
The material in this section has been adapted from Chapters 2 and 4 of my book. In these chapters, you'll also learn how to write a quantum program for the concepts you've learned about here.