Entanglement
The mega-qubit is not just a nifty bookkeeping
device to track how gates affect all possible states
at the same time.
It underpins entanglement, a central tenet of
quantum mechanics that makes a quantum computer not
just another hyper-fast computer but one that
solves problems in ways that cannot be duplicated on
classical computers.
Although superposition is a quantum phenomena, it is at least
understandable.
Entanglement, on the other hand, jars our common sense. Not
just ours though. It spooked Einstein too and he was never
able to come to grips with this concept. Yet, if you're
to write quantum algorithms, you have to learn to not only
handle this counter-intuitive feature of quantum mechanics
but to actually design algorithms that depend on it.
The mega-qubit and the qubelets model gives us a way to
to get our arms around this bizarre concept.
To understand this uniquely quantum phenomena
consider the following quantum
circuit:
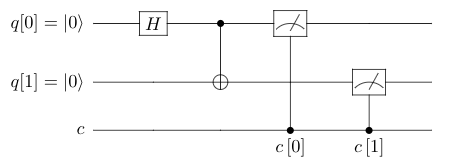
This circuit has a new gate that we talked about earlier. So, let's
review this gate and then come back to this circuit.
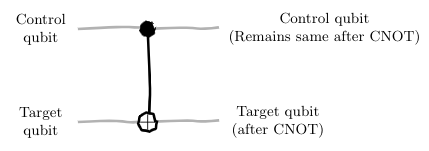
Interlude: CNOT Gate
The Controlled-NOT, or CNOT gate and its
cousins Controlled-Controlled-NOT (CCNOT)
Controlled-Controlled-Controlled-NOT (CCCNOT) gates
provide a mechanism to implement if-then type of
logic in quantum computers. The CNOT gate,
in particular, performs a NOToperation on a
designated qubit, the target if the quantum
state on another qubit, the control is $\ket{1}$.
If the quantum state on the control is $\ket{0}$,
the quantum state on the target is left alone.
The CNOT gate is shown as follows:
The following figure summarizes the operation of the CNOT
gate:
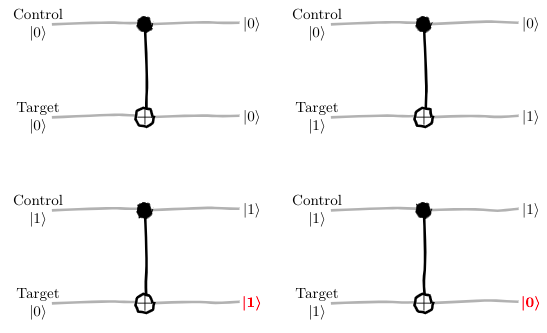
The target qubits, in the two bottom circuits highlight
that they have been switched because the control
qubit is $\ket{1}$.
Back to Disentangling Entanglement
We can now visually analyze the quantum circuit
shown in the beginning of this section. The
H gate splits the pentagon
in the top qubit so that it now has a pentagon
and a triangle.
These pair up with the pentagon in
the bottom qubit to form a mega-qubit with two
pairs, as shown on the left mega-qubit in the following
figure:
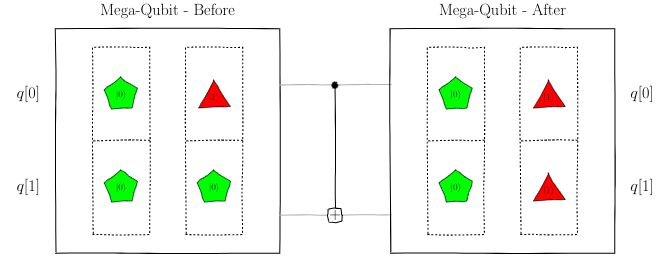
To work out the mega-qubit after the CNOT gate,
analyze each combination individually even though the
actual quantum gate acts on them simultaneously. The
new mega-qubit is the aggregate of the CNOT gate
acting on each input combination.
The top shape in each combination is fed to the CNOT gate’s
control qubit and the bottom shape is passed
to is target qubit. Since the left pair has a
pentagon on the top, it won’t be affected by the
CNOT gate. The right pair, however, has a
triangle $\ket{1}$ qubelet. Thus, the CNOT gate
will switch the bottom pentagon $\ket{0}$ qubelet to
a triangle $\ket{1}$ qubelet. As a result, the
mega-qubit on the right, after the CNOT gate
has operated on it, will have two pairs: one with
both pentagons and the other with both triangles.
When the Measure gates inspect the state of these
qubits, mega-qubit will randomly collapse to one of the two
combinations in the mega-qubit. So, either a $0$ is
logged in both classical registers or a $1$.
Key Concept
Here it comes. The final observation that'll help
you see the mystery behind entanglement.
In each case, though, if you
know the state recorded in one register, you can deduce
the state in the other without actually measuring the
second qubit. In other words — and this is the key
concept — the quantum circuit shown previously
entangles the states of the two qubits.
In fact, if you look at each qubit individually, there is
nothing to suggest that one is influencing the other.
For example, in the above figure, restrict your attention
to the bottom qubit:
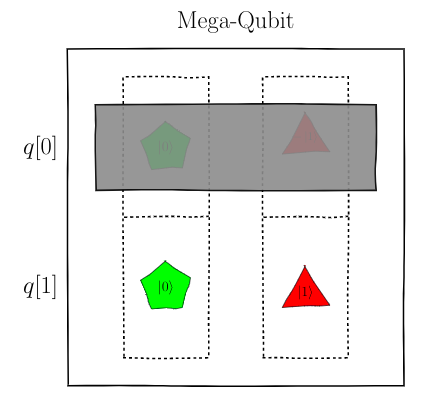
This qubit contains a pentagon $\ket{0}$ and a
triangle $\ket{1}$ qubelet. If this
qubit existed on its own, then when measured,
it'll randomly collapse to one or the other and
log a $0$ or a $1$ in the classical register.
But, the mega-qubit couples it with the top qubit.
So, if the top qubit collapses to the triangle,
the second combination in the mega-qubit is selected.
And, the bottom qubit is forced to collapse
to the triangle. In other words, the
act of measuring one qubit forces the state of the other.
This oddball behavior where the states of different
qubits are tied to each other is called
entanglement.
Because the states of
different qubits are intimately in lockstep without
any apparent physical linkage between them, this
phenomena is also called spooky action at a
distance.
As weird as it may sound, entangled qubits are a central
concept in quantum mechanics and is the root of
frustration for many scientists.
But, it's a real phenomena that has been confirmed
experimentally.
Using just two shapes — pentagons and
triangles — and a few basic operations,
we actually get to the core of
quantum computing phenomena. In fact, these are not
just superficial concepts that skirt around the
central principles of quantum computing. In my book,
I show how they are intimately tied with the
standard mathematical treatment of quantum
effects. These concepts are pivotal to build a
strong intuition of quantum effects so that you can
design algorithms for real world applications.
So, despite no one ever actually seeing a quantum state
packing two states simultaneously, you write programs
that imply multi-state qubits exist and can design
algorithms to solve ultra-hard problems.
Where to learn more
The material in this section has been adapted from Chapter 5 of my book. In this chapter, you'll also learn how to write a quantum program for the concepts you've learned about here.