Chaining Quantum Gates
If you want to learn to write quantum algorithms
that solve hard problems with blazing speed, you
will need to develop a gut feel for how
gates adjust quantum states to arrive at the
solution of your problem. To this end, in this
section, you'll see how the qubelets
concept can give you insight into what happens
to the quantum states when you chain quantum
gates together.
Consider the following quantum circuit that
chains the H, Z and another H
gate:
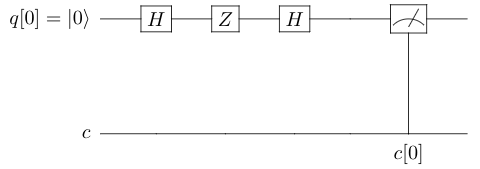
In this circuit, the $\ket{0}$ qubit in the quantum register
$q[0]$ is acted on by a sequence
of quantum gates — H, Z and H.
The resulting state of the qubit is inspected by the
Measure> gate on the right and recorded in the classical
register $c[0]$.
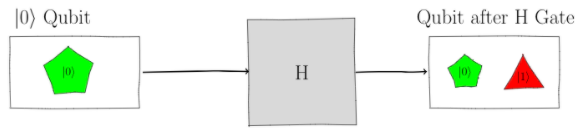
The first $H$-gate on the left splits the $\ket{0}$ qubit:
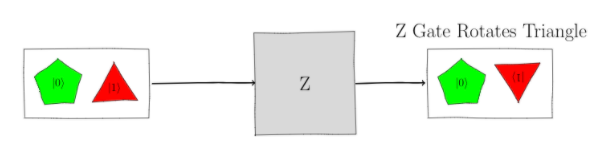
Next, the $Z$-gate rotates the triangle $\ket{1}$ qubelet by
$180^\circ$:
Finally, the $H$-gate on the right splits both the
pentagon $\ket{0}$ and the triangle $\ket{1}$:

Since the $H$-gate splits a $\ket{1}$ into a pentagon $\ket{0}$
and an inverted triangle $\ket{1}$, it'll split
an inverted triangle $\ket{1}$ into an
inverted pentagon $\ket{0}$ and an
inverted-inverted triangle $\ket{1}$. That is, a
triangle that goes back to its non-inverted orientation.
Key Concept: Canceling Qubelets
According to the rules of quantum mechanics,
a qubelet will cancel out with an inverted
qubelet of the same type. So, the inverted pentagon cancels
with the non-inverted one leaving a quantum state with 2 triangles:
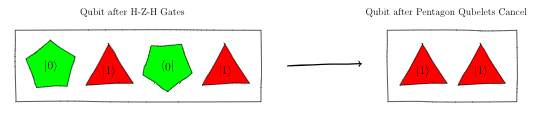
So, after the canceling of the pentagon qublets,
the quantum state only has 2 triangles. When you
measure this quantum state, since it only
has triangle $\ket{1}$ qubelets, the only classical
state this quantum state can collapse to is a 1.
In other words, no matter how many qubelets of the
same type are in a quantum state, the qubit must
always collapse to the classical bit corresponding
to that qubelet.
Thus, starting out with a pentagon $\ket{0}$
qubit, the H-Z-H sequence of gates changes
it to a triangle $\ket{1}$ qubit.
Remarkable Takeaway
What should strike you is that even
though the H gates randomly collapse
to 0 or 1, by understanding how the qubelets are
acted upon by the gates, you can precisely figure
out a chain of gates where the end result is
deterministic.
Note that all of this canceling happens
immediately without the need to invoke any special
quantum instruction.
Of course, there's only so much you can do with a
single qubit. To leverage the true power of quantum
computers, in the next section
you'll see the qubelets concept can help make sense of
multi-qubit systems.
Where to learn more
The material in this section has been adapted from Chapter 7 of my book. In this chapter, you'll also learn how to write a quantum program for the concepts you've learned about here.