Quantum Gates
The essential objective in quantum computing is to apply
physical effects — such as a precisely timed
burst of a magnetic field — to tilt the odds
that favor the quantum bit collapsing to one or the
other state.
A quantum program is a sequence of these physical
effects that takes qubits from some initial state
to one that solves the computational problem.
Fortunately, you don't need to know quantum mechanics to implement these physical effects. A standard set of devices,
called quantum gates, encapsulate the quantum principles.
These principles essentially amount to rotating the
pentagon $\ket{0}$ and triangle $\ket{1}$ qubelets.
We'll look at a few quantum gates to see how they
manipulate quantum states. Or more precisely, how
they affect the pentagon $\ket{0}$ and triangle
$\ket{1}$ qubelets.
NOT Gate
A quantum NOT gate, like its classical counterpart,
toggles the qubelet. For example, when a NOT gate acts on a
pentagon $\ket{0}$ qubelet, it switches it to a triangle
$\ket{1}$ qubelet:

Mathematically, we represent the action of the NOT
gate on the quantum states as follows:
\begin{eqnarray*}
NOT: & \ket{0} \rightarrow \ket{1} \\
NOT: & \ket{1} \rightarrow \ket{0} \\
\end{eqnarray*}
The rest of the gates you'll see in this section
are "pure" quantum gates and have no classical
equivalents.
Z Gate
The Z gate only acts on the $\ket{1}$
qubelets and flips their orientation
$180^{\circ}$. The Z gate does not act on
the pentagon $\ket{0}$ qubelets. For example, when the
Z gates on a quantum state containing a
pentagon $\ket{0}$ qubelet and a triangle
$\ket{1}$ qubelet
shown on the left in the figure below, it only
turns the triangle $\ket{1}$ upside down:

(On the right qubit, the faded triangle $\ket{1}$ behind the
triangle $\ket{1}$ in the foreground shows its original
position.)
Mathematically, we represent the action by the
Z gate as follows:
$$
Z: \frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1}
\rightarrow
\frac{1}{\sqrt{2}} \ket{0} - \frac{1}{\sqrt{2}} \ket{1}
$$
T Gate
A T gate also only acts on the triangle $\ket{1}$
qubelet but rotates the triangle $\ket{1}$ qubelet by
$45^{\circ}$ anti-clockwise:

(On the right qubit, the faded triangle $\ket{1}$ behind the
triangle $\ket{1}$ in the foreground shows its original position.)
Mathematically, we represent the action by the T
gate as follows:
$$
T: \frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1}
\rightarrow
$$
Other quantum gates, such as the $S$, $S^\dagger$
and $T^\dagger$ gates, rotate the triangle $\ket{1}$ by
other amounts.
H Gate
Quantum gates do more than just rotate qubits though. A
signature operation is to take a pure> qubit,
such as one having only a pentagon $\ket{0}$ qubelet,
and splits it so that
the qubit ends up with both pentagons and
triangles. For example, when the $H$, or Hadamard
gate, acts on a pentagon $\ket{0}$ qubit, it splits it
into a pentagon $\ket{0}$ and triangle $\ket{1}$:
image
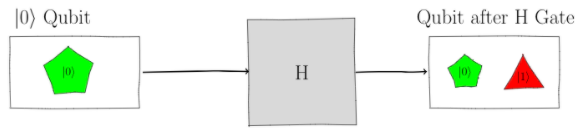
Mathematically, the action of the H gate on a $\ket{0}$
qubit is:
$$
H: \ket{0} \rightarrow
\frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1}
$$
But, it acts differently on
a $\ket{0}$ qubit than a $\ket{1}$ qubit. When it
splits a $\ket{1}$ qubit, the triangle $\ket{1}$
qubelet is inverted:
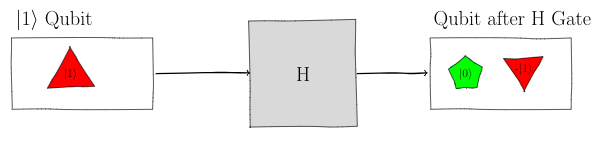
Mathematically, the action of the H gate on a $\ket{1}$
qubit is:
$$
H: \ket{1} \rightarrow
\frac{1}{\sqrt{2}}\ket{0} - \frac{1}{\sqrt{2}}\ket{1}
$$
Because the H gate can take "pure" $\ket{0}$ or
$\ket{1}$ qubit and create a quantum state with
both qubits simultaneously, the H gate is frequently
used to kickstart a quantum program.
Like classical logic gates, these form the building blocks of
quantum circuits that manipulate qubits to perform computational tasks. A quantum program encodes this circuit so that it runs on a
quantum computer. In the next section, you'll see how
chaining quantum gates lets you control how to evolve a
quantum state in your programs.
Why Do Most Quantum Gates Act on $\ket{1}$ Qubelets Only?
There's nothing special about triangle $\ket{1}$ qubelets. The quantum gates could equally well have rotated pentagon $\ket{0}$ qubelets. In quantum computing, it's only the relative difference between the rotations of a $\ket{0}$ qubelet versus that of the $\ket{1}$ qubelet. So, by convention, the quantum gates rotate the $\ket{1}$ qubelet.
Where to learn more
The material in this section has been adapted from Chapter 7 of my book. In this chapter, you'll also see the other gates you can use to split and rotate qubelets. The action of the gates are described visually giving you a deeper understanding of how these acts work on quantum bits.